Wprowadzenie do elektroniki/Półprzewodniki/Wzmacniacze Operacyjne

Wzmacniacze Operacyjne

Rozważania na temat wzmacniaczy zaczniemy od przybliżenia wzmacniacza rzeczywistego do wzmacniacza idealnego. Przybliżenie to jak się okazuje pozwala na zadowalającym poziomie analizować proste układy elektroniczne oparte o wzmacniacze.

Symbol przykładowego wzmacniacza operacyjnego

Wzmacniacz operacyjny posiada dwa wejścia. To oznaczone znakiem plus to wejście nieodwracające a oznaczone znakiem minus to wejście odwracające fazę sygnału.

Przybliżenia stosowane w analizie i opisie układów wzmacniaczy operacyjnych

1. Wzmocnienie wzmacniacza operacyjnego (różnicowe)$K_u=\mathrm{\infty }$
2. Rezystancja wejściowa wzmacniacza operacyjnego $R_{we}=\mathrm{\infty }$
3. Rezystancja wyjściowa wzmacniacza operacyjnego $R_{wy}=0$

Jeżeli rozważymy z założenia pierwsze to nasuwający się wniosek będzie taki:

Jeżeli napięcie na wejściu odwracającym będzie większe od napięcia na wejściu nieodwracającym to wówczas na wyjściu wzmacniacza będzie napięcie bliskie ujemnej wartości napięcia zasilającego. Jeżeli zaś napięcie na wejściu nieodwracającym będzie większe to wówczas wyjście wzmacniacza będzie wysterowane dodatnią wartością napięcia zasilającego.

Układy pracy wzmacniaczy Operacyjnych

W tej części zapoznamy się z podstawowymi układami w jakich można zastosować wzmacniacz operacyjny.

Wtórnik napięciowy

W tym układzie zadaniem wzmacniacza jest odwzorowaniem na wyjściu napięcia wejściowego. Korzyści jakie daje mam wtórnik napięciowy są następujące:

1. Wysoka rezystancja wejściowa samego wzmacniacza sprawia, że układ nie obciąża źródła sygnału
2. Niska rezystancja wyjściowa sprawia, że układ jest odporny na spadki napięcia spowodowane pobieraniem przez obciążenie wzmacniacza większych prądów

Zasada działania wtórnika napięciowego: Przyjmując założenie o nieskończonym wzmocnieniu samego wzmacniacza dochodzimy do wniosku, iż aby układ pozostawał w stanie stabilnym to napięcie między jego wejściem odwracającym i nieodwracającym musi być równe zeru. Dlatego w przypadku zwiększenia wartości napięcia wejściowego (na wejściu nieodwracającym) wzmacniacz zwiększy napięcie wyjściowe tak aby osiągnąć poziom równowagi $u_{wy}=u_{we}$

Wzmacniacz nieodwracający

Po niewielkiej modyfikacji układu wtórnika napięciowego otrzymamy układ wzmacniacza nieodwracającego.Schemat tego układu widzimy na rysunku poniżej.

Wyprowadzimy poniżej wzór na wzmocnienie takiego wzmacniacza.

Założeniem podobnie jak w przypadku wtórnika napięciowego będzie nieskończenie wielkie wzmocnienie samego wzmacniacza. To implikuje sytuacja w której (w stanie równowagi) napięciu na wejściach odwracającym i nieodwracającym są sobie równe $U_{we}=U_{R1}$ Z układu dzielnika napięciowego możemy łatwo wyliczyć napięcie $U_{R1}$

$U_{R1}=R1*\frac{U_{wy}}{R1+R2}$

Stąd można wyliczyć wartość napięcia wyjściowego wzmacniacza jako

$U_{wy}=\frac{R1+R2}{R1}*U_{R1}$

A ponieważ $U_{R1}=U_{we}$ wzór możemy zapisać jako

$U_{wy}=\frac{R1+R2}{R1}*U_{we}$ aby wyznaczyć wzmocnienie wzmacniacza należy obustronnie podzielić równanie przez $U_{we}$

$k_u=\frac{U_{wy}}{U_{we}}=\frac{R1+R2}{R1}=1+\frac{R2}{R1}$

Układ ten posiada te same zalety które posiada wtórnik napięciowy, ale możemy za pomocą rezystorów R1 oraz R2 regulować wzmocnienie.

Wzmacniacz odwracający

Poniżej przedstawiony układ oparty na wzmacniaczu operacyjnym już nie jest tak idealny, ponieważ rezystancja wejściowa układu zależy od rezystancji rezystorów użytych do ustawiania wzmocnienia

Wyprowadzimy wzór na wzmocnienie takiego układu (również i tu przyjmiemy założenie iż wzmocnienie napięciowe samego wzmacniacza jest równe nieskończoności) Przy takim założeniu napięcia na wejściach odwracającym i nieodwracającym są sobie równe i wynoszą 0V (Wzmacniacz musi uzyskać stan równowagi). Stąd łatwo policzyć jaki prąd będzie płynął przez rezystor R1

$I=\frac{U_{we}}{R1}$

Ponieważ idealny wzmacniacz sam w sobie nie pobiera prądu na wejściu taki sam prąd musi płynąć przez rezystor R2. Napięcie na rezystorze R2 wynosi

$U_{R_2}=I*R_2$

Napięcie na wyjściu wzmacniacza będzie miało taką samą wartość jak napięcie na rezystorze R2 ale będzie mieć przeciwny znak (Odwrócenie fazy). Z napięciowego prawa Kirchoffa wyglądało by to tak. $U_{wy}+U_{R_2}=0$ <=> $U_{wy}=-U_{R_2}$ Wejście odwracające wzmacniacza operacyjnego przyjmuje potencjał 0[V] - mówimy o punkcie masy pozornej. Dalsze obliczenia to podstawienie wzorów.

$U_{wy}=-\frac{U_{we}*R_2}{R1}$

Po podzieleniu obydwu stron równania Przez Uwe otrzymamy wzór na wzmocnienie wzmacniacza w tym układzie.

$k_u=-\frac{R_2}{R_1}$

Sumator

Wzmacniacze operacyjne możemy zatrudnić również do wykonywania pewnych operacji matematycznych na sygnałach wejściowych. Schemat układu spełniającego funkcję sumatora przedstawiono poniżej

Wyprowadzimy wzór na napięcie wyjściowe układu zakładając, że rezystory $R_1=R_2=R_3=R$

Z prądowego prawa Kirchoffa wynika, że prąd $I_3=I_1+I_2$

A z napięciowego, że $U_{wy}=-U_{R_3}<=>U_{wy}=-I_3*R_3$

Prąd $I_1=\frac{U_{we1}}{R}$ a prąd $I_2=\frac{U_{we2}}{R}$

Z tego wynika, że prąd $I_3=\frac{U_{we1}+U_{we2}}{R}$

Po podstawieniu powyższych zależności do wzoru na napięcie wyjściowe układu i przyjmując wartość rezystora $R_3=R$ otrzymamy wynik

$U_{wy}=-\frac{U_{we1}+U_{we2}}{R}*R$

Z tego wniosek iż na wyjściu takiego układu otrzymujemy napięcie równe odwróconej w fazie sumie napięć wejściowych.

$U_{wy}=-(U_{we1}+U_{we2})$

Wzmacniacz Całkujący

PMP Punkt masy pozornej

Podobnie jak w przypadkach poprzednich założymy iż wzmacniacz operacyjny jest układem idealnym Wówczas prąd płynący przez rezystor $R_1$ oraz płynący przez kondensator $C_1$ są sobie równe i możemy je obliczyć z zależności

$i(t)=\frac{u_{we}(t)}{R_1}$

Wiemy, że prąd płynący przez kondensator wyrażamy zależnością

$i(t)=\frac{dq(t)}{dt}=C_1*\frac{du(t)}{dt}$

Stąd przyrost napięcia du wyznaczamy według zależności

$du(t)=\frac{1}{C_1}i(t)dt$

po scałkowaniu równania otrzymamy zależność jak poniżej

$u(t)=\frac{1}{C_1}\underset{-\mathrm{\infty }}{\overset{t}{\int }}i(t)dt$

Napięcie wyjściowe ma przeciwny znak niż napięcie na kondensatorze

$u_{wy}(t)=-\frac{1}{C_1}\underset{-\mathrm{\infty }}{\overset{t}{\int }}i(t)dt$

Podstawiając za $i(t)$ zależność z wzoru pierwszego otrzymamy

$u_{wy}(t)=-\frac{1}{C_1}\underset{-\mathrm{\infty }}{\overset{t}{\int }}\frac{u_{we}(t)}{R_1}dt=-\frac{1}{R_1*C_1}\underset{-\mathrm{\infty }}{\overset{t}{\int }}{u}_{we}(t)dt=-\frac{1}{\tau }\underset{-\mathrm{\infty }}{\overset{t}{\int }}{u}_{we}(t)dt$

$\tau$ stała czasowa obwodu $\tau =R*C$

Jeśli przyłożymy na wejście napięcie stałe to na wyjściu otrzymamy napięcie liniowo narastające co poniżej postaram się udowodnić. Załóżmy że na wejście układu podamy sygnał opisany za pomocą funkcji skokowej [1] funkcja ta przyjmuje wartość 0 dla t<0 i wartość $U_{const}$ dla t>0; Możemy całkę oznaczoną podzielić na dwa przedziały $u_{wy}(t)=-\frac{1}{\tau }(\underset{-\mathrm{\infty }}{\overset{0}{\int }}0dt+\underset{0}{\overset{t}{\int }}{U}_{const}*1(t)dt)$

Pierwsza Całka będzie 0 więc ją pomijamy drugą całkę rozbijamy zgodnie z twierdzeniem Newtona-Leibniza [2]

$u_{wy}(t)=-\frac{U_{const}}{\tau }\underset{0}{\overset{t}{\int }}1(t)dt=-\frac{U_{const}}{\tau }(t-0)$

$u_{wy}(t)=-\frac{U_{const}}{\tau }t$

Układ stosowany do zamiany napięcia na czas np w przetwornikach analogowo-cyfrowych (pojedyncze lub podwójne całkowanie)

Wzmacniacz Różniczkujący

Zasada działania układu jest następująca: Prąd płynący przez kondensator C1 jest wyznaczony z zależności

$i_{C_1}(t)=C_1\frac{d{u}_{we}(t)}{dt}$

Napięcie wyjścowe

$u_{wy}(t)=-u_{R_1}(t)=-i_{C_1}(t)*R_1=-C_1{R}_1\frac{d{u}_{we}(t)}{dt}$

Idąc dalej

$u_{wy}(t)=-\tau u_{w^{\prime }e}(t)$

Wniosek: napięcie na wyjściu jest pochodną napięcia wejściowego

Zadanie

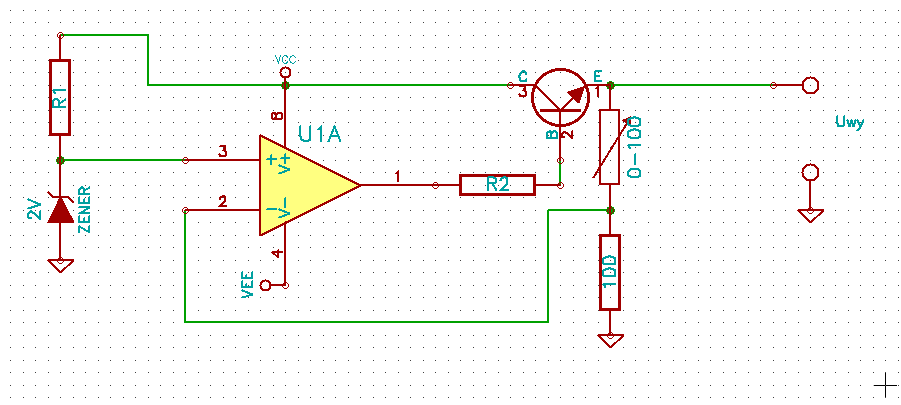
1. Układ przedstawiony na rysunku poniżej przedstawia stabilizator napięcia

Proszę policzyć w jakim zakresie będzie się zmieniało napięcie na wyjściu jeśli rezystor nastawny będzie zmieniał swoją wartość w przedziale od 0 do 100

2. Do układu całkującego przyłożono nieznane napięcie Ux i ładowano kondensator przez 10[s], Następnie przyłożono wzorcowe napięcie -1[V]. Napięcie wyjściowe układu całkującego osiągnęło wartość 0 [V] po 15[s].

Jle wynosiło nieznane napięcie Ux??